2の補数とは何か

序論

コンピュータにおける整数演算では、「2の補数」という表現方法が

事実上の標準として用いられている。

しかし多くの解説では、その計算方法や導入理由が省略され、

「2の補数とは2の補数である」という同語反復に近い説明に

留まっている場合が多い。

本節では、2の補数を数学的概念としてではなく、

「有限ビット幅しか持たない計算機が、

引き算を足し算だけで処理するために選択した表現規則」

として説明する。

本論

CPUが直面した制約

CPUは有限個のビットで数値を表現する。

例えば8ビットの場合、表現できる状態は

00000000 から 11111111 までの256通りしか存在しない。

この制約のもとで、正の数と負の数の両方を扱うには、

同じビット列に対して異なる意味を割り当てる必要がある。

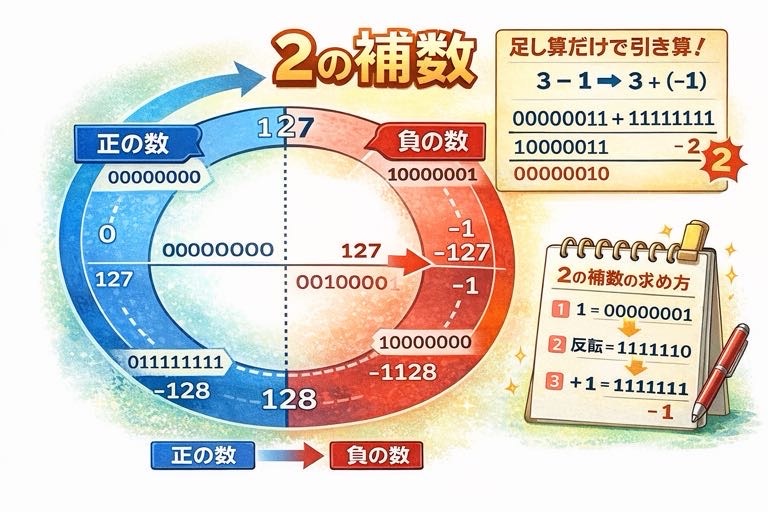
数値を円環として扱う発想

8ビット整数は、0から255まで直線的に並んでいるのではなく、

255の次に0へ戻る「円環構造」を持つと考えることができる。

この円環の前半を正の数、

後半を負の数として解釈するという規則が

2の補数表現である。

2の補数表現の割り当て

8ビットの場合、以下のように解釈される。

00000000 ～ 01111111 : 0 ～ 127
10000000 ～ 11111111 : -128 ～ -1

ビット列そのものは変化しておらず、

人間がどのように意味付けするかだけが異なる点が重要である。

2の補数の計算方法

ある正の数Xに対して、その負の数（-X）を表す

2の補数は次の手順で求められる。

Xを2進数で表す
すべてのビットを反転する
1を加算する

例として、1の2の補数は次のように計算される。

なぜ足し算だけで引き算になるのか

引き算は「負の数を足す」こととして処理される。

例えば 3 – 1 は、3 + (-1) として計算される。

  00000011
+ 11111111
-----------
1 00000010

最上位の桁あふれは破棄され、

残った 00000010 が計算結果となる。

CPUは足し算しか行っていないが、

結果として引き算が実現されている。

2の補数がもたらした効果

2の補数表現により、

CPUは足し算回路だけで

引き算や符号付き演算を処理できるようになった。

これは回路の簡素化、高速化、信頼性向上に直結する。

結論

2の補数とは、数の本質的性質ではなく、

有限ビット幅という制約の中で

計算機を単純に動作させるために選択された

工学的な表現規則である。

その仕組みを理解せずに用いると、

オーバーフローや符号反転といった境界条件で

重大な誤動作を引き起こす可能性がある。

Q&A

Q. なぜ2の補数という名前なのですか？

A. 基数が2（2進数）であり、

「基数に対する補数」を用いて

負の数を表現する方法だからです。

Q. 正の数が負の数に変わるのですか？

A. 変わりません。

ビット列は同じままで、

人間がその意味を負の数として

解釈しているだけです。

Q. CPUは本当に負の数を理解していますか？

A. 理解していません。

CPUは常にビット列の足し算をしているだけで、

負の数という概念は人間側の解釈です。

Q. なぜ計算結果が壊れることがあるのですか？

A. 有限ビット幅を超えた計算結果は

切り捨てられるため、

境界条件では人間の期待と

異なる結果になることがあります。

宇宙誕生の少し前から宇宙終焉の少し先までを数で表す論文

recent posts

about